Teaching Kids Programming – Recursive Algorithms to Balance a Binary Search Tree

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

How to Balance a Binary Search Tree (Examples)

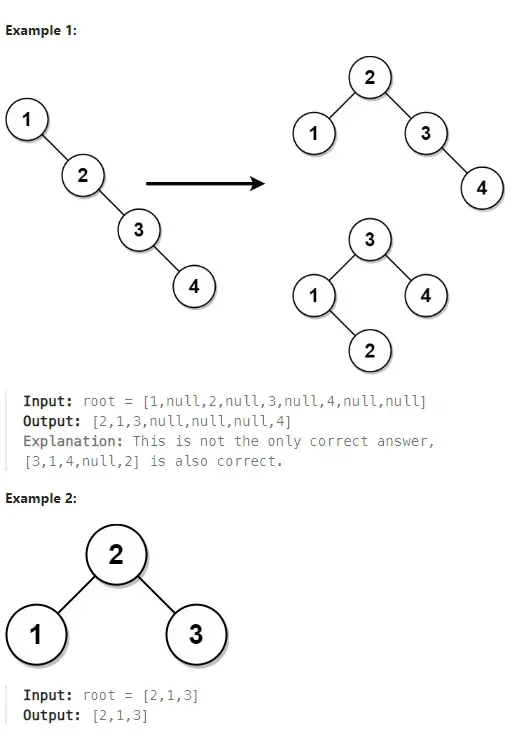
Example 1:
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:
Input: root = [2,1,3]
Output: [2,1,3]

Constraints:
The number of nodes in the tree is in the range [1, 104].
1 <= Node.val <= 105

Recursive Algorithms to Balance a Binary Search Tree

We need two steps to balance a binary search tree (BST). First step is to convert it to a sorted list by performing an inorder traversal. And then the second step is to recursively construct the Balanced Version of the same BST by choosing the middle one as the root.

A Binary Tree can be represented using the following Class (Python):

1
2
3
4
5
6

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

In-order Traversal Algorithm to Convert to a Sorted List

There are a few ways (and implementations) to perform a In-order traversal algorithm on a Binary (Search) Tree. The idea is to visit the left tree nodes, and then the current node (root), and then the nodes on the right tree. We can do this via Recursion or Iterative approach. Below is a cleaner approach using the yield keyword (iterator/generator).

1
2
3
4
5
6

def dfs(root):
    if not root:
        return
    yield from dfs(root.left)
    yield root.val
    yield from dfs(root.right)

def dfs(root):
    if not root:
        return
    yield from dfs(root.left)
    yield root.val
    yield from dfs(root.right)

Build a Balanced Binary Search Tree from a Sorted List (Recursion)

Once we have a sorted list, we can divide the left and right tree by the middle number as the root, and then we recursively divide the subarray into two, left and right, until we have only one node which should be a leaf node. The following is the complete source code to build a balance binary search tree from a BST.

We use two pointers to improve the efficiency rather than array slicing which should incur extra space/time complexity. The Left and Right pointers denote a subarray of numbers to pick when building a sub Binary Search Tree.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
 
        def dfs(root):
            if not root:
                return
            yield from dfs(root.left)
            yield root.val
            yield from dfs(root.right)
 
        arr = list(dfs(root))
 
        def f(L, R):
            if L > R:
                return
            if L == R:
                return TreeNode(arr[L])
            ## find the middle, e.g. M = (L + R) // 2
            M = L + R >> 1
            root = TreeNode(arr[M])
            root.left = f(L, M - 1)
            root.right = f(M + 1, R)
            return root
 
        return f(0, len(arr) - 1)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:

        def dfs(root):
            if not root:
                return
            yield from dfs(root.left)
            yield root.val
            yield from dfs(root.right)

        arr = list(dfs(root))

        def f(L, R):
            if L > R:
                return
            if L == R:
                return TreeNode(arr[L])
            ## find the middle, e.g. M = (L + R) // 2
            M = L + R >> 1
            root = TreeNode(arr[M])
            root.left = f(L, M - 1)
            root.right = f(M + 1, R)
            return root

        return f(0, len(arr) - 1)

The time complexity for both recursions are O(N). The space complexity is also O(N) due to Recursion Calling Stack.

Teaching my Kids at Microsoft Office Whiteboard – Day 624 – Balance a Binary Search Tree (Aug, 2023)

–EOF (The Ultimate Computing & Technology Blog) —