Teaching Kids Programming – Recursive Depth First Search Graph Algorithm to Determine a Strongly Connected Component

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given n cities represented as an integer in [0, n) and a list of one-way roads that connects one city to another.

Return whether you can reach any city from any city.

Constraints
n ≤ 10,000
m ≤ 100,000 where m is the length of roads

Example 1
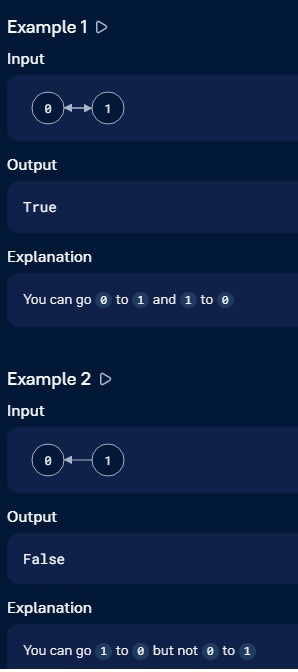
Input

1 2 3 4 5

n = 2 roads = [     [0, 1],     [1, 0] ]

n = 2
roads = [
    [0, 1],
    [1, 0]
]

Output
True
Explanation
You can go 0 to 1 and 1 to 0

Example 2
Input

1 2 3 4

n = 2 roads = [     [1, 0] ]

n = 2
roads = [
    [1, 0]
]

Output
False
Explanation
You can go 1 to 0 but not 0 to 1

Hints:
Reverse the direction of every edge in the graph. How does this help?
There should be only 1 strongly connected component
Kosaraju’s Algorithm

Recursive Depth First Search Graph Algorithm to Determine a Strongly Connected Component

A SCC (Strongly Connected Component) means that any vertices in a Directed Graph can be reachable from any vertices. It is easier to check for a Undirected Graph – we just have to check if the Undirected graph is connected as one piece.

To proof any vertex can go to any vertex, we can check the following two:

1. Vertex 1 (for simplicity) can go to any other vertex – this can be done via a single Depth First Search.
2. Any vertex can go to vertex 1 – this can be done via a Single Depth First Search Algorithm on the reversed Graph (with reverse edges).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def solve(self, n, roads):        
        def f(cur, G):
            seen = set()
            def dfs(cur):
                if cur in seen:
                    return
                seen.add(cur)
                for i in G[cur]:
                    dfs(i)            
            dfs(cur)
            return len(seen) == n
        G1 = defaultdict(list)
        for a, b in roads:
            G1[a].append(b)        
        G2 = defaultdict(list)
        for a, b in roads:
            G2[b].append(a)
        return f(0, G1) and f(0, G2)

class Solution:
    def solve(self, n, roads):        
        def f(cur, G):
            seen = set()
            def dfs(cur):
                if cur in seen:
                    return
                seen.add(cur)
                for i in G[cur]:
                    dfs(i)            
            dfs(cur)
            return len(seen) == n
        G1 = defaultdict(list)
        for a, b in roads:
            G1[a].append(b)        
        G2 = defaultdict(list)
        for a, b in roads:
            G2[b].append(a)
        return f(0, G1) and f(0, G2)

We are performing the DFS twice – and thus the time complexity is O(V+E) and the space complexity is also O(V+E) where V and E are the number of the vertex and edges respectively.

–EOF (The Ultimate Computing & Technology Blog) —