Teaching Kids Programming – Shortest Path Algorithms by Iterative Deepening Search (IDS), Depth First Search (DFS) or Breadth First Search (BFS) on Undirected Graphs

Teaching Kids Programming: Videos on Data Structures and Algorithms

Shortest Path on Undirected Graphs: DFS or BFS?

The Depth First Search and Breadth First Search algorithms can be both used to traverse a Graph (including trees). The BFS uses a queue and we can guarantee the shortest path once a node is visited as we traverse the paths in the level-by-level order. The Python code for BFS a Graph is as follows where we need to use a hash set to remember the nodes that have been pushed to the queue (visited). We use deque to have O(1) constant pop operation of the queue.

1
2
3
4
5
6
7
8
9
10

def BFS(G, src):
    q = deque([src])
    seen = set()
    while q:
        cur = q.popleft()
        visit(cur)     # visiting node cur
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
                q.append(n)

def BFS(G, src):
    q = deque([src])
    seen = set()
    while q:
        cur = q.popleft()
        visit(cur)     # visiting node cur
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
                q.append(n)

If we want to find a shortest path between src and target (stop when we hit target):

1
2
3
4
5
6
7
8
9
10
11
12
13

def BFS(G, src, target):
    q = deque([src])
    seen = set()
    while q:
        cur = q.popleft()
        visit(cur)     # visiting node cur
        if cur == target:
            return True
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
                q.append(n)
    return False

def BFS(G, src, target):
    q = deque([src])
    seen = set()
    while q:
        cur = q.popleft()
        visit(cur)     # visiting node cur
        if cur == target:
            return True
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
                q.append(n)
    return False

The Depth First Search Algorithm uses a stack – which usually is implemented by Recursion. The Python code for traversing a Graph using a DFS is:

1
2
3
4
5
6
7

def dfs(G, src, seen):
    if src in seen:
        return
    visit(src)     # visiting node src
    seen.add(src)
    for n in G[src]:
        dfs(G, n, seen):

def dfs(G, src, seen):
    if src in seen:
        return
    visit(src)     # visiting node src
    seen.add(src)
    for n in G[src]:
        dfs(G, n, seen):

And, if we want to stop after we find the target:

1
2
3
4
5
6
7
8
9
10
11

def dfs(G, src, seen, target):
    if src in seen:
        return False
    if src == target:
        return True
    visit(src)     # visiting node src
    seen.add(src)
    for n in G[src]:
        if dfs(G, n, seen):
            return True
    return False

def dfs(G, src, seen, target):
    if src in seen:
        return False
    if src == target:
        return True
    visit(src)     # visiting node src
    seen.add(src)
    for n in G[src]:
        if dfs(G, n, seen):
            return True
    return False

Is BFS with Stack DFS?

If we use stack instead of queue in BFS – does it become a DFS? considering the following modified BFS (with stack instead):

1
2
3
4
5
6
7
8
9
10

def BFS(G, src):
    q = [src] # list - used as the stack
    seen = set()
    while q:
        cur = q.pop()
        visit(cur)     # visiting node cur
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
                q.append(n)

def BFS(G, src):
    q = [src] # list - used as the stack
    seen = set()
    while q:
        cur = q.pop()
        visit(cur)     # visiting node cur
        for n in G[cur]:
            if n not in seen:
                seen.add(n)
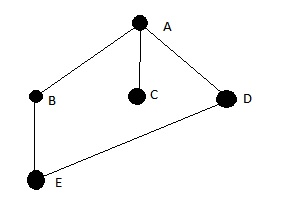
                q.append(n)

And considering the following Simple Graph aka a Graph with no multiple edges and no loops – and if we start with vertex A:

A simple graph with five vertex ABCDE

For BFS, we have traversal order: ABCDE (level by level). For DFS: we have ABEDC. But with BFS that is implemented using stack – we have ABECD (there is a difference in marking a node visited when pushing or being visited).

Therefore, a Breadth First Search that is implemented with stack is not equivalent to a Depth First Search Algorithm.

Can DFS guarantee a shortest Path?

No in general unless we use DFS to exhaustive all the search paths. Considering the following simple graph (a Triangle):

    A
   / \
  B---C

The shortest path from A to B is AB however with DFS, the first path is ACB.

Iterative Deepening Search Algorithm

The Iterative Deepening Search (IDS) is based on DFS however it guarantees a shortest path. Let’s take a look:

1
2
3
4
5
6
7
8
9
10
11

def dfs(G, src, target, seen, depth, maxDepth):
    if src in seen:
        return False
    # only difference than a DFS
    if depth > maxDepth:
        return False
    if src == target:
        return True
    seen.add(src)
    for n in G[src]:
        dfs(G, n, seen, depth + 1, maxDepth)

def dfs(G, src, target, seen, depth, maxDepth):
    if src in seen:
        return False
    # only difference than a DFS
    if depth > maxDepth:
        return False
    if src == target:
        return True
    seen.add(src)
    for n in G[src]:
        dfs(G, n, seen, depth + 1, maxDepth)

We add depth parameters so that we can stop search when the search distance exceeds a threshold. And we start with depth 1 and increment the distance until the target is found:

1
2
3
4
5
6

def ids(G, src, target):
   found = False
   while not found:
       seen = set()
       depth += 1
       found = dfs(G, src, target, seen, 0, depth)       

def ids(G, src, target):
   found = False
   while not found:
       seen = set()
       depth += 1
       found = dfs(G, src, target, seen, 0, depth)       

Let’s consider this simple Graph again.

    A
   / \
  B---C

When depth is one, we can only find the paths A-C and A-B. We stop at C when doing DFS at max depth 1. Thus, this approach Iterative Deepening Search guarantees the shortest path.

IDS uses linear space complexity for some graphs considering a Full Binary Tree where the BFS need to use exponential 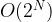space when the full binary tree is depth N e.g. there are leaves nodes when the full binary tree has depth N. In some chess playing e.g. MinMax Tree, the IDS may actually be a bit faster considering the searches at lower-depth limit may improve the cache hits.

Shortest Path Algorithms

• Teaching Kids Programming – Distance Between Bus Stops (Floyd Warshal Shortest Path in Simple Undirected Weighted Regular Graph)
• Teaching Kids Programming – Depth First/Limit Search and Iterative Deepening Search Algorithm on Unweighted Graph
• Teaching Kids Programming – A Light Talk on Breadth First Search, Uniform Cost Search and Dijkstra Shortest Path Graph Algorithms
• Teaching Kids Programming – Introduction to Dijkstra Single Source Shortest Path Graph Algorithm
• Teaching Kids Programming – Single Source Shortest Path Algorithm in a Directed Unweighted Graph using Breadth First Search
• Teaching Kids Programming – Floyd Warshal Multi-source/All Pairs Shortest Path Algorithm (Sum of Costs in a Directed Unweighted Graph)
• Teaching Kids Programming – Uniform Cost Search Algorithm to Solve Single-Source Shortest Path in a Graph
• Teaching Kids Programming – Shortest Path Algorithms by Iterative Deepening Search (IDS), Depth First Search (DFS) or Breadth First Search (BFS) on Undirected Graphs
• Teaching Kids Programming – Finding the Network Delay Time via Floyd-Warshall Shortest Path Algorithm
• Teaching Kids Programming – Distance Between Bus Stops (Shortest Distance in Simple Undirected Weighted Regular Graph)

–EOF (The Ultimate Computing & Technology Blog) —