Teaching Kids Programming – Sum of Distinct Positive Factorial Numbers

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given a positive integer n, return whether n can be written as the sum of distinct positive factorial numbers.

Example 1
Input
n = 31
Output
True
Explanation
Since 31 = 4! + 3! + 1!

Example 2
Input
n = 4
Output
False
Explanation
Since 4 = 2! + 2! but not distinct.

Example 3
Input
n = 6
Output
True
Example 4
Input
n = 29
Output
False

Hints:
Can we generate all factorials up to n?
super increasing sequence knapsack

Algorithm to Check Sum of Distinct Positive Factorial Numbers

The sum of all factorials up to f(i) is always smaller than f(i+1):

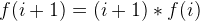which is bigger than
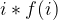and 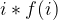is bigger or equal to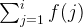
And thus: 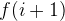is larger than

We then can greedly subtract the largest factorial number that is less or equal to n until we can’t. If the remainder is zero then we can use the distinct factorial numbers to sum up to n. If we try the smallest factorial number first, we may risk to reduce the sum too early and including a higher sum may not be possible.

We pre-compute the factorials and store them in array which is O(N) space and time. And then starting from the largest number, we try to reduce the sum.

1
2
3
4
5
6
7
8
9
10
11
12

class Solution:
    def factorialSum(self, n):
        fact = x = 1
        res = []
        while fact <= n:
            fact *= x
            res.append(fact)
            x += 1
        for i in range(len(res) - 1, -1, -1):
            if n >= res[i]:
                n -= res[i]
        return n == 0

class Solution:
    def factorialSum(self, n):
        fact = x = 1
        res = []
        while fact <= n:
            fact *= x
            res.append(fact)
            x += 1
        for i in range(len(res) - 1, -1, -1):
            if n >= res[i]:
                n -= res[i]
        return n == 0

Given n is a signed 32-bit number, there are 12 distinct factorials within this range i.e. 12!=479001600 which is the largest factorial in 32-bit signed range. Therefore The time complexity is O(12)=O(1). And so is space complexity.

And we can use the Recursive Depth First Search Algorithm to pick or not pick each item: Teaching Kids Programming – Sum of Distinct Positive Factorial Numbers via Depth First Search Algorithm

Sum of Distinct Positive Factorial Numbers:

• Teaching Kids Programming – Sum of Distinct Positive Factorial Numbers
• Algorithms to Sum using Distinct Positive Factorial Numbers
• Teaching Kids Programming – Sum of Distinct Positive Factorial Numbers via Depth First Search Algorithm

–EOF (The Ultimate Computing & Technology Blog) —