Teaching Kids Programming – Algorithms to Find the Unique Vertex of Zero Indegree in a Directed Acyclic Graph

Teaching Kids Programming: Videos on Data Structures and Algorithms

There are n teams numbered from 0 to n – 1 in a tournament; each team is also a node in a DAG. You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph. A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a. Team a will be the champion of the tournament if there is no team b that is stronger than team a. Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes
A cycle is a series of nodes a1, a2, …, an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, …, an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
A DAG is a directed graph that does not have any cycle.

A Directed Acyclic Graph (DAG)

Example 1:
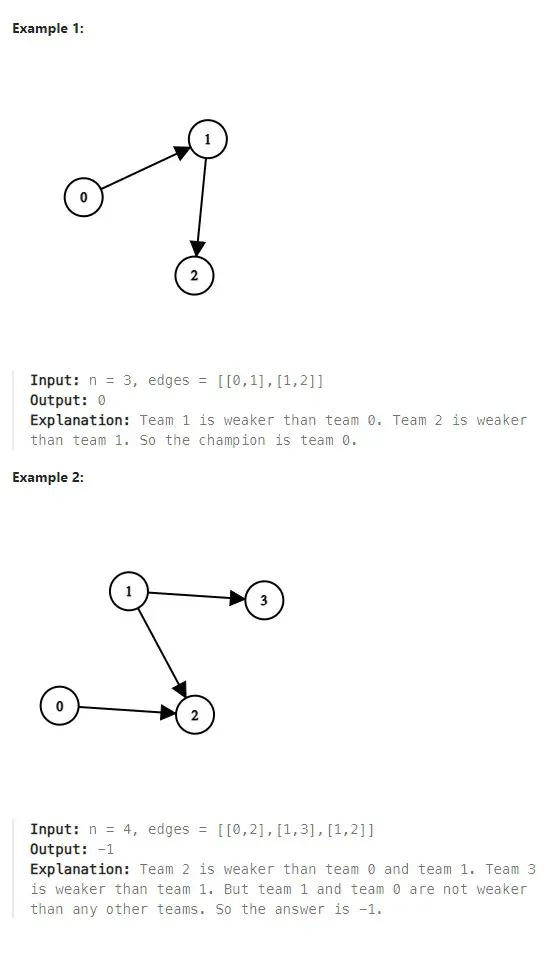
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.

Example 2:
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.

Constraints:
1 <= n <= 100
m == edges.length
0 <= m <= n * (n – 1) / 2
edges[i].length == 2
0 <= edge[i][j] <= n – 1
edges[i][0] != edges[i][1]
The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

Algorithms to Find the Unique Vertex of Zero Indegree in a Directed Acyclic Graph

Similar to Teaching Kids Programming – Algorithms to Find the Vertex of Zero Indegree in a Directed Acyclic Graph, we can find the vertices that have zero indegrees (no incoming edges), and then check if there is only one which we return it otherwise we return -1.

1
2
3
4
5
6
7

class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        ind = defaultdict(int)
        for a, b in edges:
            ind[b] += 1
        x = [i for i in range(n) if ind[i] == 0]
        return x[0] if len(x) == 1 else -1

class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        ind = defaultdict(int)
        for a, b in edges:
            ind[b] += 1
        x = [i for i in range(n) if ind[i] == 0]
        return x[0] if len(x) == 1 else -1

Here is another way of getting the single/unique vertex which does not have any incoming edges. We can put all the vertices that have at least one incoming edge in a set, and compute the sum. If there are exactly n-1 vertices, then we can compute the sum difference between the total sum aka 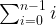and the sum(v) where v is the vertex set which have non-zero indegree.

1
2
3
4
5
6

class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        weak = {b for a, b in edges}
        if len(weak) < n - 1:
            return -1
        return n * (n - 1) //2 - sum(weak)

class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        weak = {b for a, b in edges}
        if len(weak) < n - 1:
            return -1
        return n * (n - 1) //2 - sum(weak)

We are given the Graph as a list of the edges, rather than Adjacency Matrix or Adjacency List.

–EOF (The Ultimate Computing & Technology Blog) —