Teaching Kids Programming – Converting (Binary) Trees to Undirectional Graphs via DFS and BFS Algorithms

Teaching Kids Programming: Videos on Data Structures and Algorithms

Define Binary Trees in Python

Trees can be considered as DAG (Directed Acyclic Graph) – the Directed means that we usually can only visit child nodes from parent nodes and not vice versa. The Trees can usually be represented in Object Oriented manner:

1
2
3
4
5

class TreeNode:
    def __int__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class TreeNode:
    def __int__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Trees are Subset of Graphs

Trees are subsets of Graphs, so sometimes it can be represented by list of edges. The Graph G is a collection of vertex V and edges E, i.e. 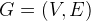. A graph can be represented by adjacent matrix or adjacent list:

Define Graphs in Adjacent Matrix

Give vertex 0 to n-1 we can allocate a two dimensional list where G[i][j] is the weight of the edge from vertex i to vertex j.

For example, given Graph: 1–>2–>0, we can define the G in the following:

1
2
3
4
5

G = [
  [0, 0, 0],
  [0, 0, 1],
  [1, 0, 0]
]

G = [
  [0, 0, 0],
  [0, 0, 1],
  [1, 0, 0]
]

0 means no edge, and 1 means edge, we can also replace the value with the weight if it is a weighted Graph. The values on the diagonals mean the vertex to itself usually 0.

Define Graphs in Adjacent List

The Graph can be also declared using Adjacent List where G is a defaultdict where the default value type is a list. And the keys are vertex. For example, given undirectional graph: 0-2-1 we can define G as following:

1
2
3
4
5

G = {
 0: [2],
 1: [2],
 2: [0, 1]
}

G = {
 0: [2],
 1: [2],
 2: [0, 1]
}

For weighted graphs, we can store the list of tuples where each tuple is the vertex and the weight.

Convert Binary Trees to Undirectional Graph in Adjacent List

If the trees are defined as a list of edges, it should be trivial to convert to graph:

1
2
3
4
5
6

def convertToGraph(edges):
    G = defaultdict(list)
    for a, b in edges:
        G[a] += [b]
        G[b] += [a]
    return G

def convertToGraph(edges):
    G = defaultdict(list)
    for a, b in edges:
        G[a] += [b]
        G[b] += [a]
    return G

If the trees are stored in class TreeNode, we need to traverse the tree using either Depth First Search (DFS) or Breadth First Search (BFS) Algorithm.

For DFS, we need to pass down the parent in recursion:

1
2
3
4
5
6
7
8
9
10

def convertBinaryTreeToGraph(root):
    G = defaultdict(list)
    def dfs(root, parent):
        if not root:
            return
        if parent:
            G[root] += parent
            G[parent] += root
        dfs(root.left, root)
        dfs(root.right, root)

def convertBinaryTreeToGraph(root):
    G = defaultdict(list)
    def dfs(root, parent):
        if not root:
            return
        if parent:
            G[root] += parent
            G[parent] += root
        dfs(root.left, root)
        dfs(root.right, root)

If we go for BFS, we can use a deque (double-ended queue) and for each node we push (enque) to the queue, it will be a tuple that contains the node and its parent:

1
2
3
4
5
6
7
8
9
10
11
12
13

def convertBinaryTreeToGraph(root):
    G = defaultdict(list)
    q = deque([(root, None)])
    while q:
        cur, parent = q.popleft()
        if parent:
            G[cur] += [parent]
            G[parent] += [cur]
        if cur.left:
            q.append((cur.left, cur))
        if cur.right:
            q.append((cur.right, cur))
    return G

def convertBinaryTreeToGraph(root):
    G = defaultdict(list)
    q = deque([(root, None)])
    while q:
        cur, parent = q.popleft()
        if parent:
            G[cur] += [parent]
            G[parent] += [cur]
        if cur.left:
            q.append((cur.left, cur))
        if cur.right:
            q.append((cur.right, cur))
    return G

–EOF (The Ultimate Computing & Technology Blog) —