A Recursive Full Permutation Algorithm in Python

The full permutation of a list can be easily programmed using recursive algorithms. The number of the full permutation results is where 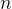is the number of elements to permutate.

A quick implementation is possible using recursive functions. Recursive programming is easy to implement, and the algorithm is clear to represent. However, the computation efficiency of recursive functions may not be good enough.

The recursive function is the one who calls itself. In order to avoid ending infinitely, there will usually be conditions (according to parameters passed into the recursive function), for functions to jump out to non-recursive function. For example, the can be computed recursively using the below python function.

1
2
3
4
5
6
7

def test(n):
    if n == 1:
        # jump out of recursive function
        return 1
    else:
        # split into smaller problems, recursively
        return n * test(n - 1)

def test(n):
    if n == 1:
        # jump out of recursive function
        return 1
    else:
        # split into smaller problems, recursively
        return n * test(n - 1)

The full permutation of list can be solved by picking any element, placing it in the first, and recursively solving the smaller problem.

1
2
3
4
5
6
7
8
9
10
11

#!/usr/bin/env python
def perm(n, i):
    if i == len(n) - 1:
        print n
    else:
        for j in range(i, len(n)):
            n[i], n[j] = n[j], n[i]
            perm(n, i + 1)
            n[i], n[j] = n[j], n[i] # swap back, for the next loop
        
perm([1, 2, 3], 0)

#!/usr/bin/env python
def perm(n, i):
    if i == len(n) - 1:
        print n
    else:
        for j in range(i, len(n)):
            n[i], n[j] = n[j], n[i]
            perm(n, i + 1)
            n[i], n[j] = n[j], n[i] # swap back, for the next loop
        
perm([1, 2, 3], 0)

The ending condition will be to check whether the index reaches the rightmost (we’ve zero-length list). Otherwise, loop each element and make it the left-most of the current permutated list; recursively jump into the smaller problem where the index advances one step.

It is also interesting to find that in Python, swapping two variables does not need a third temporarily variable. Instead, simply using tuple assignment will be enough.

1
2
3
4

a = 2
b = 3
a, b = b, a
print a, b # 3, 2

a = 2
b = 3
a, b = b, a
print a, b # 3, 2

The output of the above full permutation algorithm is:

1
2
3
4
5
6

[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 2, 1]
[3, 1, 2]

[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 2, 1]
[3, 1, 2]

The C++ version of the above Python permutation algorithm is described in this post: C++ Coding Reference: next_permutation() and prev_permutation()

You may also want to refer to C++ Coding Reference: next_permutation() and prev_permutation() for more advanced topics on permutation algorithms.

See also: Teaching Kids Programming – Recursive Permutation Algorithm

Permutations and Combinations

• Using Bitmasking Algorithm to Compute the Combinations of an Array
• Teaching Kids Programming – Recursive Backtracking Algorithm to Compute the Combinations
• Teaching Kids Programming – Recursive Permutation Algorithm
• Teaching Kids Programming – Introduction to Permutation and Combination
• Teaching Kids Programming – Three Algorithms to Compute the Combination Number
• A Recursive Full Permutation Algorithm in Python
• The Permutation Iterator in Python
• GoLang: Full Permutation Command Line Tool
• The Permutation Algorithm for Arrays using Recursion
• Full Permutation Algorithm Implementation in BASH

–EOF (The Ultimate Computing & Technology Blog) —