Teaching Kids Programming – Max Number of Connected Components in a Directed Graph (Detonate the Maximum Bombs) via Recursive Depth First Search Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb.

The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range.

You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range. These bombs will further detonate the bombs that lie in their ranges.

Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb.

Detonate the Maximum Bombs

Example 1:
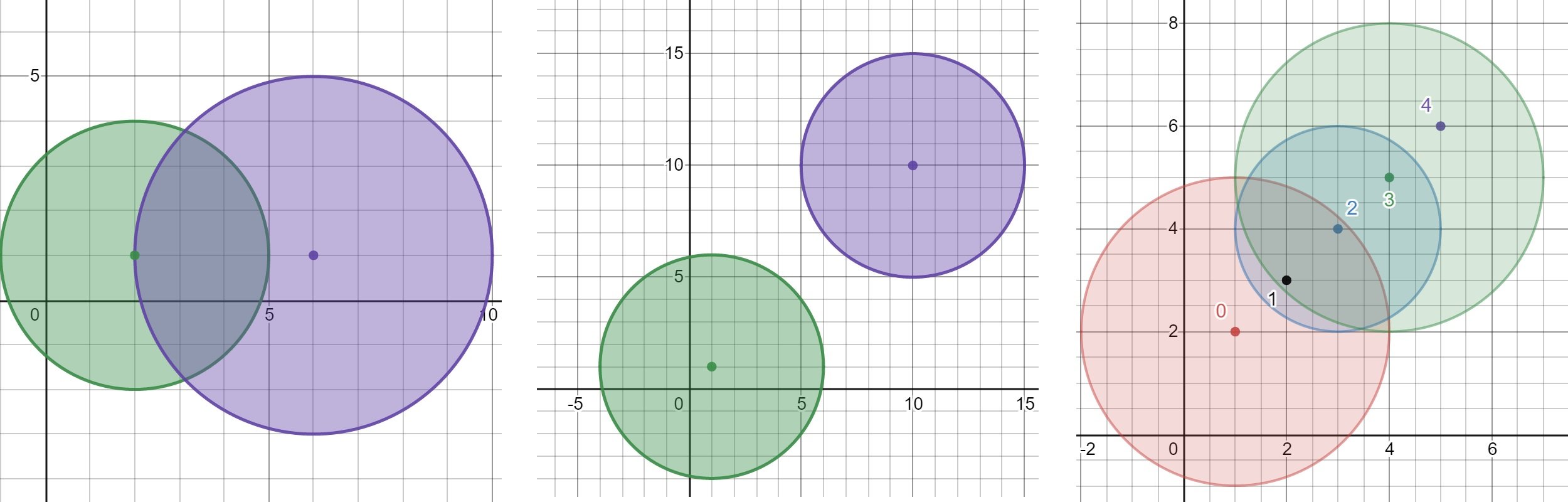
Input: bombs = [[2,1,3],[6,1,4]]
Output: 2
Explanation:
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.

Example 2:
Input: bombs = [[1,1,5],[10,10,5]]
Output: 1
Explanation:
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.

Example 3:
Input: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
Output: 5
Explanation:
The best bomb to detonate is bomb 0 because:
– Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
– Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
– Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.

Constraints:
1 <= bombs.length <= 100
bombs[i].length == 3
1 <= xi, yi, ri <= 10^5

Max Number of Connected Components in a Directed Graph (Detonate the Maximum Bombs)

When we detonate bomb A, bomb B is detonated, but that doesn’t mean vice versa. Therefore, this is a Directed Graph problem, and we aim to find the maximum number of a connected components (vertices) in this Directed Graph.

We can perform a Depth First Search (DFS) or a Breadth First Search (BFS) graph traversal algorithm.

To check if we ignite bomb A, can we also ignite bomb i.e. if there is an edge from vertex A to vertex B, we check the radius of vertex A to see if it is far enough to cover the center of the vertex B.

1
2
3
4

def f(a, b):
    x1, y1, r1 = a
    x2, y2, _ = b
    return (x1-x2)**2 + (y1-y2) **2 <= r1**2

def f(a, b):
    x1, y1, r1 = a
    x2, y2, _ = b
    return (x1-x2)**2 + (y1-y2) **2 <= r1**2

We also need to construct a Directed Graph using the Adjacency List, so we can follow the edges from a vertex easily. And we also need to keep a hash table to store the vertices that we have visited so far so we don’t end up in a cycle. But this hash table needs to be reset when we try a new DFS traversal from a new vertex source.

The time complexity is O(N^3) as there are N vertices to start DFS from, and each DFS takes O(N^2) time. The space complexity is O(N^2) as we need to have a Adjacency List to store the Directed Graph (also a hash table O(N) and Recursion takes O(N) space).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def maximumDetonation(self, bombs: List[List[int]]) -> int:
 
        G = defaultdict(list)
        n = len(bombs)
        for i in range(n):
            for j in range(n):
                if i != j and f(bombs[i], bombs[j]):
                    G[i].append(j)
 
        def dfs(x, seen):
            if x in seen:
                return 0
            seen.add(x)
            ans = 1
            for y in G[x]:
                ans += dfs(y, seen)
            return ans
 
        ans = 0        
        for i in range(n):
            seen = set()
            ans = max(ans, dfs(i, seen))
        return ans

class Solution:
    def maximumDetonation(self, bombs: List[List[int]]) -> int:

        G = defaultdict(list)
        n = len(bombs)
        for i in range(n):
            for j in range(n):
                if i != j and f(bombs[i], bombs[j]):
                    G[i].append(j)

        def dfs(x, seen):
            if x in seen:
                return 0
            seen.add(x)
            ans = 1
            for y in G[x]:
                ans += dfs(y, seen)
            return ans

        ans = 0        
        for i in range(n):
            seen = set()
            ans = max(ans, dfs(i, seen))
        return ans

We can do this in a shorter way (one liner):

1

return max((dfs(i, set()) for i in range(n)), default=0)

return max((dfs(i, set()) for i in range(n)), default=0)

We can solve this using Breadth First Search Algorithm (BFS): Teaching Kids Programming – Breadth First Search Algorithm to Compute the Maximum Number of Connected Components in a Directed Graph (Detonate the Maximum Bombs)

–EOF (The Ultimate Computing & Technology Blog) —