Derangement Permutation Implementation using R Programming

Given N natural integers (from 1 to N), the number of all permutations is N! (Factorial). That is explained by the fact: There are N choices when selecting the first number, (N-1) choices selecting the second number and so on, until the last number to select at last position. So the answer would be .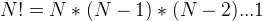

The derangement Permutation adds an important rule i.e. The number i cannot be placed at i-th position. For example, 321 is not a derangement permutation because the number 2 is at 2-nd position but 312 is because each number is not in its original position.

In combinatorial mathematics, a derangement is a permutation of the elements of a set, such that no element appears in its original position. You are given an integer n. There is originally an array consisting of n integers from 1 to n in ascending order, return the number of derangements it can generate.

Example 1:
Input: n = 3
Output: 2
Explanation: The original array is [1,2,3]. The two derangements are [2,3,1] and [3,1,2].

Example 2:
Input: n = 2
Output: 1

Dynamic Programming

We denote the answer for N numbers by F(N). When we place the number N, obviously, we cannot place it at N-th position, we can place N at (N-1) positions e.g. 1 to N-1. Assume we place N at K-th position. Now, where do we put the K? We can swap it with N (at last position), so the permutation will be F(n-2). If not, then there are N-1 numbers to do the derangement permutation, which will be F(n-1). So the final answer will be:

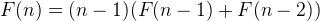
Terminating conditions: F(1) = 0, F(2) = 1.

Recursion in R programming

With this straightforward recurrence formula, we can implement a recursive function in R language.

f = function(n) {
  if (n == 1) {
     0
  } else if (n == 2) {
     1
  } else {
     (n-1) * (f(n - 1) + f(n - 2))
  }
}

The first few derangement permutations numbers are:

> n=1:10
> Map(f, n)
[[1]]
[1] 0

[[2]]
[1] 1

[[3]]
[1] 2

[[4]]
[1] 9

[[5]]
[1] 44

[[6]]
[1] 265

[[7]]
[1] 1854

[[8]]
[1] 14833

[[9]]
[1] 133496

[[10]]
[1] 1334961

We use the Map function to convert a vector to another based on the mapping function. However, the recursion has the problem of performance issues, which tends to be very slow and causing the stack overflow when the input size is large. Therefore, it is better to re-write the recursion using the iterative approach.

f = function(n) {
  a = 0
  b = 1
  if (n == 1) {
     a
  } else if (n == 2) {
     b
  } else {
    for (i in 3:n) {
       c = (i-1) * (a + b)
       a = b
       b = c
    }
    b
  }
}

The iterative implementation is highly efficient because it does not re-compute the intermediate results over and over again (and it does not make recursive calls).

General Formula

F(n) can be simplified to via induction:

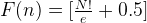
R Tutorial

• R Tutorial – Map, Filter, Reduce, Lambda
• R Tutorial – Monte Carlo
• R Tutorial – Permutation
• R Tutorial – Sigmoid
• R Tutorial – Connecting to STEEMSQL via RODBC
• R Tutorial – How rich is SteemIt Wechat Group?
• R Tutorial – Knowing when a Steem Whale vote?
• R Tutorial – How to Connect to SteemSQL via RStudio?
• R Tutorial – Using R to Fit Linear Model – Predit Weight over Height

Derangement Algorithms

• Teaching Kids Programming – Dynamic Programming Algorithms to Compute the Number of Derangement Permutations
• Derangement Permutation Implementation using R Programming
• Teaching Kids Programming – (!3+3)*!3=10 – Derangement Algorithms via Dynamic Programming Algorithm

–EOF (The Ultimate Computing & Technology Blog) —